A growing number of weather stations means large amount of meteorological data are produced every year (Steinacker et al.[1]; Delvaux et al.[2]). These meteorological data are used to analyze the possible impacts of climate change on environment, validate climate model simulations and provide initial conditions for numerical weather prediction (Feng et al.[3]; Schneider et al.[4]; Zhao et al.[5]; Chan et al.[6]). However, surface temperature observations are easily affected by the relocation of stations and instrument failure (Hubbard et al.[7]; Martins et al.[8]); such factors influence the accuracy of surface observations. Therefore, quality control for surface temperature observations is essential to atmospheric sciences (Cheng et al.[9]). Currently, quality control is not only an important part of data acquisition, transmission and processing, but also a precondition for international exchange of meteorological data and products (Xu et al.[10]; Beges et al.[11]; Xiong et al.[12]; Li et al.[13]).
Quality control (QC) for a single station mainly include extreme value check (Grant[14]; Mann et al.[15]; Schwab et al.[16]; Aldukhov and Chernykh[17]), internal consistency check (Reek et al.[18]; Zhang et al. [19]; Shao et al.[20]) and temporal outlier check (Fiebrich et al.[21]; Ye et al.[22]). These quality control methods for a single station strongly depend on the integrity of the observations, which is based on the time series used for quality control. Quality control methods for a single station are not effective if observations are missing for a long period. Recently, the use of multiple stations in quality control has proven useful partly due to an increasing number of observation stations (Eischeid et al.[23]; Bannister[24]). Normally, quality control methods for multiple stations mainly include the spatial regression test method (SRT), the inverse distance weighting method (IDW) and polynomial interpolation (OI). Besides, SRT and IDW are the most widely used methods used for the surface temperature quality control. The main idea of the SRT and IDW methods is to estimate the value of the target station based on neighboring stations. The difference between the IDW method and the SRT method is the choice of weights between different neighboring stations. The SRT method has been found to be superior to the IDW method because the root-mean-square error is more effective for determining the weights of neighboring stations (You et al.[25]). In addition, the OI and SRT methods are consistent with the statistical information needed for quality control, as OI calculates the background field and uses a two-error covariance matrix to analyze the sensitivity of the target station observations based on statistical surface meteorological observations and the background field. A Bayesian QC method (BQC) calculates the probability of error of the observations from the perspective of pure mathematics compared with other quality control methods (Ingleby et al.[26]; Zhu et al.[27]). BQC provides quality control for surface meteorological observations by calculating the posterior probability of gross error. Particularly, a probabilistic spatiotemporal approach based on a spatial regression test provided a quantitative probability to indicate the uncertainty of data (Xu et al.[28]; Cerlini et al.[29]). It is meaningful and changes the traditional concept of "right" or "wrong" in meteorological observations quality control (Choi et al.[30]; Liu et al.[31]), and it also proves the reliability of the SRT method.
Most of traditional QC methods are based on mathematical or statistical methods (While et al.[32]). When mathematical or statistical methods fail to explain why the performance of a QC method for one station is affected by the terrain and climate, intelligent algorithms may be used instead. For example, the SRT method is still affected by the geographical environment of the target station and neighboring stations, and there is no specific formula to explain such impacts. SRT offers the advantage of selecting the neighboring stations with the smallest error and weighting neighboring stations according to historical data, but it is unable to use the regression method incorporating the observations of neighboring stations. Therefore, this article proposes to combine the random forest method (RF), which is more efficient for regression, with the SRT method which is used to preprocess the dataset. Then, the dataset is trained by the RF method, and the estimated value of the target station is obtained by using the SRF method.
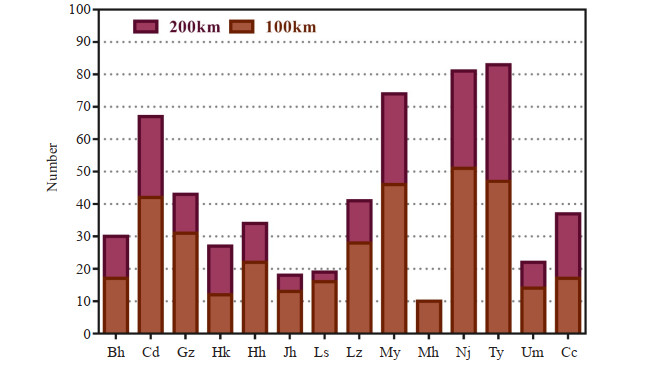
Daily mean temperature observations from 14 target stations from 2005 to 2014 are selected, and the numbers of the neighboring stations are shown in Fig. 1. The 14 target stations are abbreviated as follows: Beihai (Bh), Chengdu (Cd), Guangzhou (Gz), Haikou (Hk), Hohhot (Hh), Jinghong (Jh), Lhasa (Ls), Lanzhou (Lz), Miyun (My), Mohe (Mh), Nanjing (Nj), Taiyuan (Ty), Urumqi (Um) and Changchun (Cc). The neighboring stations selected are within 100 km or 200 km from the target station. Fig. 2 shows that there is a significant difference in altitude among Ls, Lz and Um, where Bh, Gz, Hk and Jh are in coastal regions and Hh, Jh, Ls and Lz in high altitude regions. The distribution of surface automatic weather stations is determined by the environment and economy of China. The 14 target stations selected in this article are basically located in provincial capitals, which are economic and political centers. They are distributed in different provinces in China, covering different climates and geographical conditions of China.
The dataset used in this article is compiled by the Chinese National Meteorological Center and quality controlled by some basic quality control methods. In order to test the performance of the SRF method, artificial errors are randomly inserted into the observations from the target station (Hubbard[7]). Approximately 3% of observations are selected for the insertion of random errors, and the formula is shown in
| kλ=sλ⋅pλ | (1) |
where k is the value of the insertion error, s is the standard deviation of the observations from the target station, λ is the position for error insertion, and p is a random number with a uniform distribution with a range of ±3.5.
The spatial regression test (SRT) assigns weight according to the root-mean-square error between the target station and each of the neighboring stations. For each neighboring station, a linear regression based on an estimate is used:
| xi=ai+bi⋅yi | (2) |
where xi is the estimate of the target station, the data of ith neighboring station (i = 1, 2, …, n) is yi, ai and bi are the regression coefficients, and the weighted estimate x' is obtained by using the standard error of estimate s:
| x′=√∑Ni=1x2i⋅s−2i∑Ni=1s2i | (3) |
where N is the number of neighboring stations used. Then, the weighted standard error of estimate s' is calculated as follows:
| s′−2=N−1N∑i=1s−2i | (4) |
The confidence intervals are formed as follows:
| x′−fs′⩽x⩽x′+fs′ | (5) |
where f is the quality control parameter. If the relation in (5) holds, the observations pass the test.
The random forest (RF) method belongs to the category of ensemble learning. Schapire developed the probably approximately correct (PCA) learning model, which evaluates strong and weak learning concepts (Borchmann et al.[33]). Random forests combine multiple weak-classifier decision trees with a strong classifier, which is much easier than searching for a strong classifier directly. A random forest is a combination of tree predictors, such that each tree depends on the values of a random vector sampled independently with the same distribution for all trees in the forest (Gomes et al.[34]). For each tree, the random forest selects the training set by the self-help sampling method (Bootstrap), the test set is the samples which are not extracted, and the error estimation is based on the out-ofbag (OOB) estimation. The random forest method can be used for classification and regression. When the dependent variable Y is categorical variable, the model is classified; when the dependent variable Y is a continuous variable, the model is regression. The independent variable X can be a mixture of multiple continuous variables and multiple categorical variables.
Given an ensemble of classifiers h1(x),h2(x)⋯hk(x), and with the training set drawn randomly from the distribution of the random vector Y, X, define the margin function as formula (6):
| mg(X,Y)=avkI(hk(K)=Y)−maxj≠YavkI(hk(K)=j) | (6) |
where I (∙) is the indicator function. The margin measures the extent to which the average number of votes at Y, X for the right class exceeds the average vote for any other class. The larger the margin, the more confidence in the classification. The generalization error is given by:
| PE∗=PX,Y(mg(X,Y)<0) | (7) |
where the subscripts Y, X indicate that the probability is over the Y, X space. With the increasing number of trees during the construction of the RF models, the generalization error of almost all sequences converges to an upper limit. The upper limit is given by:
| PX,Y(P(hk(X)=Y)−maxj≠YP(hk(K)=j)<0) | (8) |
For a random forest, the upper limit of the generalization error is a method to measure the accuracy of a single classifier and the dependency between the classifiers. An upper bound for the generalization error is given by:
| PE∗⩽ˉρ(1−s2)/s2 | (9) |
where ˉρ is the mean value of the correlation. Although the bound is likely to be loose, it fulfills the same suggestive function for random forests as VC-type bounds do for other types of classifiers. It shows that the two ingredients involved in the generalization error for random forests are the strength of the individual classifiers in the forest, and the correlation between them in terms of the raw margin functions.
Generally, no overfitting situation, strong ability to resist noise and estimate the importance of features are the advantages of RF. These advantages are mainly due to the randomness of the selection of the samples and the features. However, the RF method still needs to be upgraded, for example, there is no suitable solution to the choice of mtry in random forests.
The RF method grows an ensemble of trees, and each node split is selected randomly from among the best splits; hence, it has strong generalization ability and avoids over-fitting. In the surface meteorological observations, not all neighboring stations have a strong correlation with target stations, and the neighboring stations with weak correlation are equivalent to the weak input of the datasets. Data types with many weak inputs are difficult for typical classifiers, such as neural nets and trees. Thus, the RF method is more suitable for surface meteorological observations. By using random feature selection in addition to bagging, the generalization error is estimated by out-of-bag (OOB) estimation, obtaining concrete results from otherwise theoretical values of strength and correlation. The quality control method was constructed by the SRT and RF methods, and the SRF method can be divided into the following steps. First, dataset L is divided into the training sample Ltrain and testing sample Ltest.The RMSE of ith neighboring stations si is calculated by using formula (2) and formula (12), according to the weighting coefficient, to calculate the new dataset L' :
| L′i=si∑Ni=1si⋅Li | (10) |
where N is the number of neighboring stations to be used in the new dataset. Then, the RF regression method is used to train and regress the new dataset. Ultimately, the values predicted by the SRF method yest are compared with observations of the target station (yobs) that have inserted artificial errors. Coefficient f is used to test whether the observed values fall within the confidence intervals:
| ‖yest −yobs ‖⩽f⋅σ | (11) |
If the observations of the target station fall within the confidence intervals, the observations pass the SRF test. Fig. 3 illustrates the specific flow of the SRF algorithm.
The root mean square error (RMSE), mean absolute error (MAE) and nash-sutcliffe model efficiency coefficient (NSC) are used to evaluate the performance of different methods in this article. Average differences can be described by RMSE or MAE, as RMSE and MAE are among the best overall measures of model performance. MAE and RMSE take the following forms:
| RMSE=√∑ni=1(yobs −yest )2n | (12) |
| MAE =1n⋅n∑i=1‖yobs −yest ‖ | (13) |
| NSC =1−∑ni=1(yobs −yest )2n∑i=1(yobs −ˉy)2 | (14) |
where yobs is the observations of the target station, yest is the estimated value of the target station, and ˉy is the arithmetic mean of yobs for the test sample i = 1, 2, …, n.
In meteorological data quality control research, a type I error is the incorrect rejection of a true null hypothesis, while a type II error is the failure to reject a false null hypothesis. More simply stated, a type I error is detecting an effect that is not present, while a type II error is failing to detect an effect that is present. In order to balance the two types of errors, Xiong[12] utilized a mean-square ratio of detected errors to the total number of seeds (MSR) to evaluate the performance of the method. Also, MSR is employed to evaluate different quality control methods in this article, which is defined as follows:
| MSR=1−((α⋅r21)+r22)0.5 | (15) |
where r1 is the probability of the type I error, r2 is the probability of the type II error, and α is the weight of r1.
In this article, daily mean temperature observations from 2005 to 2013 from 14 target stations and their neighboring stations are selected as a training sample, while the 2014 observations are selected as the testing sample. It is necessary to analyze the spatial correlation of the 14 target stations and neighboring stations because the spatial correlation of all stations in a region within 200 km may impact the performance of the quality control model. As shown in Table 1, the results of the spatial correlation are calculated with a semi-variogram (Hanke et al.[35]; Gunst[36]; Maddox and Robert[37]; Deng et al.[38]) and Moran's I (Yuan et al.[39]). When R2 and I are close to 1, a smaller RSS and larger z-value is associated with higher spatial correlation between stations. It is clear that there are high spatial correlations of Bh, Cd, Gz, Hh, My, Ty and Cc, while the spatial correlations of Jh, Ls, Lz, Mh and Um are very low. The information for the 14 target stations is shown in Fig. 4, where the stations are represented by five-pointed star and the number next to the stations' name indicate the number of neighboring stations. The spatial correlation between the target station and neighboring stations are indicated as"high", "low"and "unknown". As the number of neighboring stations for Mh is too small, analyzing the semi-variogram in Mh is not possible. An assessment of the different methods for different target stations shows that spatial correlation does impact the quality control of temperature observations (Chen et al.[40]).
| Co | Co+C | Ao | R2 | RSS | I | E(I) | mean | sd | z-value | |
| Bh | 0.101 | 0.715 | 1.17 | 0.848 | 0.095 | 0.649 | -0.031 | -0.032 | 0.097 | 7.031 |
| Cd | 0.153 | 2.398 | 1.22 | 0.849 | 1.2 | 0.721 | -0.015 | -0.012 | 0.071 | 10.39 |
| Gz | 0.188 | 1.163 | 2.07 | 0.922 | 0.076 | 0.581 | -0.023 | -0.023 | 0.093 | 6.47 |
| Hk | 0.157 | 0.781 | 1.53 | 0.804 | 0.085 | 0.478 | -0.037 | -0.037 | 0.118 | 4.348 |
| Hh | 0.004 | 2.85 | 0.61 | 0.843 | 2.72 | 0.545 | -0.029 | -0.026 | 0.112 | 5.096 |
| Jh | 0.001 | 2.385 | 0.3 | 0.326 | 13.3 | 0.162 | -0.091 | -0.083 | 0.158 | 1.556 |
| Ls | 0.01 | 6.4 | 0.55 | 0.385 | 79.5 | -0.08 | -0.1 | -0.103 | 0.179 | 0.125 |
| Lz | 0.83 | 4.403 | 0.55 | 0.489 | 4.4 | 0.143 | -0.24 | -0.023 | 0.094 | 1.178 |
| My | 0.51 | 9.029 | 1.48 | 0.876 | 6.55 | 0.729 | -0.013 | -0.013 | 0.065 | 11.43 |
| Mh | / | / | / | / | / | -0.411 | -0.333 | -0.349 | 0.29 | -0.211 |
| Nj | 0.145 | 0.606 | 4.01 | 0.355 | 0.071 | 0.552 | -0.12 | -0.013 | 0.066 | 8.602 |
| Ty | 0.001 | 4.516 | 1.8 | 0.929 | 2.25 | 0.648 | -0.012 | -0.013 | 0.067 | 9.809 |
| Um | 0.01 | 11.58 | 1.54 | 0.371 | 375 | 0.446 | -0.046 | -0.046 | 0.123 | 4.014 |
| Cc | 0.269 | 1.069 | 1.38 | 0.736 | 0.287 | 0.615 | -0.027 | -0.027 | 0.104 | 6.174 |
10 neighboring stations were selected as the reference stations for prediction by using the SRT method. It was unknown whether prediction would be improved with the 10 reference stations when the SRT method was combined with the RF method. Therefore, it was necessary to identify the appropriate number of selected neighboring stations to determine whether observations of reference stations should be weighted. Fig. 5(a-c) shows the performance of the RF, SRT and SRF methods when 5, 10, 15, and 20 neighboring stations with lowest standard error were selected as reference stations, where reference stations represented as SRF5, SRF10, SRF15 and SRF20. The performances of the SRF and RF methods were found to be superior to the SRT method, as the SRF method required less time to run than the RF method did. To achieve improved quality control, 15 reference stations were selected and weighted according to performance and runtime. Since the number of neighboring stations in Jh, Ls and Mh was less than 15, the three target stations were tested separately, and the results are shown in Fig. 5(d-f), where the values of MAE in Jh, Ls and Mh are 3.448, 2.747 and 1.276 and the values of RMSE in Jh, Ls and Mh are 3.555, 2.927 and 1.736. The results show that the SRF and RF methods have better performance than the SRT method does in regions with a low density of neighboring stations. Moreover, the MAE and RMSE obtained by the SRF method were much lower than that by the SRT method, this is also consistent with Hubbard' s description of the SRT method which does not apply to stations with few neighboring stations.
In the process of spatial consistency quality control, the selection of the radius of neighboring stations also affects quality control. Thus, different radii of neighboring stations were selected for testing. Fig. 6 depicts the performance difference of the RF, SRF and SRT methods, where the MAE and RMSE obtained by the RF and SRF method were lower than those by the SRT method, and the runtime of the SRF method was less than that of the RF method with the increase of radius. The performance of the SRT method fluctuates greatly when the radius to neighboring stations is less than 80 km. It indicates that the SRT method relies on the radius of neighboring stations, while the SRF method is not affected by the radius of neighboring stations. In addition, the performance and runtime of the SRF method are relatively stable regardless of the change in radius.
Compared with the RF method, the SRF method can exploit the advantages of the SRT method to extract the most important information to construct a dataset with higher correlation, reducing the runtime of the quality control method while maintaining accuracy. The comprehensive comparison of the performance of the SRT, RF and SRF methods in Fig. 6 demonstrates that the SRF method is superior to the SRT and RF methods with the same number of selected neighboring stations and selected radius.
The performances of the RF, SRF and SRT methods in different target stations are shown in Fig. 7, which illustrates that the SRF method is superior to the RF and SRT methods. On one hand, the runtime of the SRF method is less than the RF method, particularly for regions with a large number of neighboring stations. On the other hand, the MAE and RMSE obtained by the SRF method are smaller than the SRT method, especially for regions with few neighboring stations, such as Jh, Ls and Lz, which have low spatial correlation. By comparing the performance of the three methods, it is found that the SRF method has an improved runtime over the RF method and improved accuracy in comparison to the SRT method.
It is important to note that the SRF method performs much better than the SRT method, indicating that the density of neighboring stations has a considerable impact on the performance of the SRT method; however, the density of neighboring stations has little effect on the performance of the SRF method. In addition, the SRF method has a lower MAE and RMSE than the SRT method in the regions with a large number of neighboring stations. In general, the SRF method is more stable and accurate than the SRT method as the number of neighboring stations changes, and the SRF method is more time efficient than the RF method in regions with a large number of neighboring stations.
The MAE and RMSE obtained by the SRT method were lower than the SRF method for the Hh and Um. To confirm whether this is a particular case or not, it was necessary to analyze the performance of the SRT and SRF methods for the Hh and Um. The performances of the SRT and SRF methods are shown in Fig. 8, where the diamond indicates the station with a performance of the SRT method that is better than the SRF method and the dot indicates the opposite situation and different colors in Fig. 8 indicate altitude. It is clear that the performance of the SRF method is better than the SRT method for most cases, but there are 9 stations in these two regions for which the performance of the SRT method is better than the SRF method. In the future, the selection of the quality control methods for these 9 stations is worth considering.
In this article, we proposed MSR to evaluate the QC methods, which can deal with the associated trade-offs between the two types of errors. Fig. 9 provides the MSR results of RF, SRT and SRF for different cases, which shows that the SRF can yield a higher MSR than other two methods for all cases. The MSR obtained by RF and SRT are close to each other, and there is no statistical difference except in Hh and Nj. According to Fig. 9, the performance of three methods for the region with high spatial correlations is considerably better than that for the low spatial correlations regions, but SRF is more stable. That is because RF and SRT is sensitive to spatial correlations. Also Fig. 10 illustrates the performance of the three methods with the mean and standard deviation for high spatial correlations regions and low spatial correlations regions. For all the cases, the SRF can yield a good MSR (more than 0.5), obviously outperforming the RF method and the SRT method. Fig. 10(a) shows the SRT method is slight better the RF method in high spatial correlations regions, but on the contrary, RF is better than SRT in low spatial correlations regions (Fig. 10(b)).
For geographical reasons, not all stations have the ideal number of neighboring stations, which affects the traditional models. In order to check the quality control performance of the SRF method in the specific regions, 6 regions with their neighboring stations were selected. The distribution of stations in the 6 regions is shown in Fig. 11, where the transparent area indicates the ocean or beyond borders where cannot pace the surface weather station.
Figure 12 compares the performance of the SRF and SRT methods in the 6 regions, illustrating that the SRF method has better accuracy and stability than the SRT method does. The performance of SRF is similar to that of the SRT method for Gz, Hk and Mh in Fig. 7. However, the performance of SRF is superior to that of the SRT method in the regions of Gz, Hk and Mh in Fig. 12, because the SRT method is more easily affected by the geographical environment than the SRF method. The performance of the SRF method is much better than the SRT method in the regions with few neighboring stations, such as Jh, Ls and Mh. This result illustrates that the SRF method has better stability than the SRT method does.
A new quality control method is proposed to identify the outliers in daily surface temperature observations. The key to the SRF method is the data preprocessing via the SRT method and the regression of the RF method. The SRT method can effectively select neighboring stations of high correlation, namely feature extraction; random forest has the advantages of high precision and low generalization error. For small sample data, random forest has better performance. A validation study by daily temperature observations in 14 target stations with seeded errors illustrates the excellent performance of the SRF method with spatial consistency quality control, especially for the regions with few neighboring stations.
Traditional spatial consistency quality control methods have much to do with the geographical environment of stations; the runtime of the RF method is influenced by the dataset and it increases with the increase of neighboring stations. By considering the spatial correlation coefficients and performance of different methods, it is clear that spatial correlation may greatly affect the performance of the quality control method. For example, the performance of different methods used for Bh, Cd, Gz, My and Ty is much better than the different methods used for Jh, Ls, Lz, Mh and Um. However, in some special stations such as Nj and Hk, it is difficult to determine its spatial correlation by using spatial correlation coefficients, but the performance of the SRF and SRT methods is well. The performance of Mh, which has the lowest spatial correlation, has a lower MAE and RMSE than those of Jh and Ls. Therefore, the results show that spatial correlation may have an impact on the performance of the quality control model, and there is no linear relationship between them.
However, the SRF method has some limitations. (1) The SRF method does not effectively reduce the runtime and improve the model accuracy compared with the RF method in the regions of few neighboring stations such as Jh, Ls and Mh. (2) The SRF method does work in the target stations with fewer than 15 (or 10) neighboring stations. For example, there is no difference between the performance of the SRF method and RF method in Mh because the stations filtering function of the SRT method does not make sense when the neighboring stations are fewer than 15 (or 10). (3) The SRF method evaluates the validity of the observations by thresholding, and simply divides the observations into correct or erroneous ones. Actually, the method of representing observations as credible probabilities is more reliable.
It is recommended that the SRF method could be used for the target stations with large number of neighboring stations. In future work, other regression method and interpolation method will be selected to improve the accuracy of model especially under extreme weather conditions such as typhoons. Furthermore, time series effects have not been added to the model discussion; in future research, a model that combines temporal and spatial can be considered.
Table 1 The spatial correlation indexes for the regions of the 14 target stations.
| Co | Co+C | Ao | R2 | RSS | I | E(I) | mean | sd | z-value | |
| Bh | 0.101 | 0.715 | 1.17 | 0.848 | 0.095 | 0.649 | -0.031 | -0.032 | 0.097 | 7.031 |
| Cd | 0.153 | 2.398 | 1.22 | 0.849 | 1.2 | 0.721 | -0.015 | -0.012 | 0.071 | 10.39 |
| Gz | 0.188 | 1.163 | 2.07 | 0.922 | 0.076 | 0.581 | -0.023 | -0.023 | 0.093 | 6.47 |
| Hk | 0.157 | 0.781 | 1.53 | 0.804 | 0.085 | 0.478 | -0.037 | -0.037 | 0.118 | 4.348 |
| Hh | 0.004 | 2.85 | 0.61 | 0.843 | 2.72 | 0.545 | -0.029 | -0.026 | 0.112 | 5.096 |
| Jh | 0.001 | 2.385 | 0.3 | 0.326 | 13.3 | 0.162 | -0.091 | -0.083 | 0.158 | 1.556 |
| Ls | 0.01 | 6.4 | 0.55 | 0.385 | 79.5 | -0.08 | -0.1 | -0.103 | 0.179 | 0.125 |
| Lz | 0.83 | 4.403 | 0.55 | 0.489 | 4.4 | 0.143 | -0.24 | -0.023 | 0.094 | 1.178 |
| My | 0.51 | 9.029 | 1.48 | 0.876 | 6.55 | 0.729 | -0.013 | -0.013 | 0.065 | 11.43 |
| Mh | / | / | / | / | / | -0.411 | -0.333 | -0.349 | 0.29 | -0.211 |
| Nj | 0.145 | 0.606 | 4.01 | 0.355 | 0.071 | 0.552 | -0.12 | -0.013 | 0.066 | 8.602 |
| Ty | 0.001 | 4.516 | 1.8 | 0.929 | 2.25 | 0.648 | -0.012 | -0.013 | 0.067 | 9.809 |
| Um | 0.01 | 11.58 | 1.54 | 0.371 | 375 | 0.446 | -0.046 | -0.046 | 0.123 | 4.014 |
| Cc | 0.269 | 1.069 | 1.38 | 0.736 | 0.287 | 0.615 | -0.027 | -0.027 | 0.104 | 6.174 |
| [1] |
STEINACKER R, MAYER D, STEINER A. Data quality control based on self-consistency[J]. Mon Wea Rev, 2010, 139(12): 3974-3991, https://doi.org/10.1175/mwr-d-10-05024.1.
|
| [2] |
DELVAUX C, INGELS R, VRABEL V, et al. Quality control and homogenization of the belgian historical temperature data[J]. Int J Climatol, 2019, 39(1): 157-171, https://doi.org/10.1002/joc.5792.
|
| [3] |
FENG Song, HU Qi, QIAN Wei-hong. Quality control of daily meteorological data in China, 1951-2000: a new dataset[J]. Int J Climatol, 2010, 24(7): 853-870, https://doi.org/10.1002/joc.1047.
|
| [4] |
SCHNEIDER U, BECKER A, FINGER P, et al. GPCC's new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle[J]. Theor Appl Climatol, 2014, 115 (1-2): 15-40, https://doi.org/10.1007/s00704-013-0860-x.
|
| [5] |
ZHAO Hong, ZOU Xiao-lei, QIN Zheng-kun. Quality control of specific humidity from surface stations based on EOF and FFT-Case study[J]. Front Earth Sci, 2015, 9(3): 381-393, https://doi.org/10.1007/s11707-014-0483-2.
|
| [6] |
CHAN P W, WU N G, ZHANG C Z, et al. The first complete dropsonde observation of a tropical cyclone over the South China Sea by the Hong Kong Observatory[J]. Weather, 2018, 73(7): 227-234, https://doi.org/10.1002/wea.3095.
|
| [7] |
HUBBARD K G, YOU Jin-sheng. Sensitivity analysis of quality assurance using the spatial regression approach-a case study of the maximum/minimum air temperature[J]. J Atmos Oceanic Technol, 2005, 22(10): 1520-1530, https://doi.org/10.1175/jtech1790.1.
|
| [8] |
MARTINS F R, LIMA F L, COSTA R S, et al. The seasonal variability and trends for the surface solar irradiation in northeastern region of Brazil[J]. Sustain Energy Techn, 2019, 35: 335-346, https://doi.org/10.1016/j. seta.2019.08.006. DOI: 10.1016/j.seta.2019.08.006
|
| [9] |
CHENG A R, LEE T H, KU H I, et al. Quality control program for real-time hourly temperature observation in Taiwan[J]. J Atmos Oceanic Technol, 2016, 33(5): 953-976, https://doi.org/10.1175/jtech-d-15-0005.1.
|
| [10] |
XU Zhi-fang, WANG Yi, FAN Guang-zhou. A two-stage quality control method for 2-m temperature observations using biweight means and a progressive EOF analysis [J]. Mon Wea Rev, 2013, 141(2): 798-808, https://doi.org/ 10.1175/mwr-d-11-00308.1.
|
| [11] |
BEGES G, DRNOVSEK J, BOJKOVSKI J, et al. Automatic weather stations and the quality function deployment method[J]. Meteorol Appl, 2015, 22: 861-866, https://doi.org/10.1002/met.1508.
|
| [12] |
XIONG X, YE Xiao-ling, ZHANG Ying-chao. A quality control method for surface hourly temperature observations via gene-expression programming[J]. Int J Climatol, 2017, 37(12): 4364-4376. https://doi.org/10.1002/joc.5092.
|
| [13] |
LI Hao-rui, DING Wei-yu, XUE Ji-shan, et al. A preliminary study on the quality control method for guangdong GPS/PWV data and its effects on precipitation forecasts in its annually first raining season[J]. J Trop Meteor, 2016, 22(4): 535-543, https://doi.org/10.16555/j.1006-8775.2016.04.008.
|
| [14] |
GRANT P R. Evolution, climate change, and extreme events[J]. Sci, 2017, 357(6350): 451-452, https://doi.org/10.1126/science.aao2067.
|
| [15] |
MANN M E, RAHMSTORF S, KORNHUBER K, et al. Influence of anthropogenic climate change on planetary wave resonance and extreme weather events[J]. Sci Rep, 2017, 7(1): 45242, https://doi.org/10.1038/srep45242.
|
| [16] |
SCHWAB M, STORCH H V. Developing criteria for a stakeholder-centred evaluation of climate services: the case of extreme event attribution for storm surges at the german baltic sea. meteorology hydrology and water management[J]. Res Operat Appl, 2018, 6: 1-10, https://doi.org/10.26491/mhwm/76702.
|
| [17] |
ALDUKHOV O A, CHERNYKH I V. Long-term variations in wind speed in the atmospheric layer of 0-2 km over the russian arctic from radoisonde data for 1964-2016[J]. Russ Meteorol Hydro, 2018, 43(6): 379-389, https://doi.org/10.3103/S1068373918060055.
|
| [18] |
REEK T, DOTY S R, OWEN T W. A deterministic approach to the validation of historical daily temperature and precipitation data from the cooperative network[J]. Bull Am Meteorol Soc, 1992, 73(6): 753-762, https://doi.org/10.1175/1520-0477.
|
| [19] |
ZHANG Ming-yang, ZHANG Li-feng, ZHANG Bin, et al. Assimilation of MWHS and MWTS radiance data from the FY-3A satellite with the POD-3DEnVar method for forecasting heavy rainfall[J]. Atmo Res, 2019, 219 (5): 95-105, https://doi.org/10.1016/j. atmosres.2018.12.023. DOI: 10.1016/j.atmosres.2018.12.023
|
| [20] |
SHAO Min, ZHANG Yu, XU Jian-jun. Impact of vertical resolution, model top and data assimilation on weather forecasting--a case study[J]. J Trop Meteor, 2020, 26(1): 73-83, https://doi.org/10.16555/j.1006-8775.2020.007.
|
| [21] |
FIEBRICH C A, CRAWFORD K C. The impact of unique meteorological phenomena detected by the Oklahoma Mesonet and ARS Micronet on automated quality control [J]. Bull Am Meteorol Soc, 2001, 82(10): 2173-2187, https://doi.org/0.1175/1520-0477. DOI: 10.1175/1520-0477(2001)082<2173:TIOUMP>2.3.CO;2
|
| [22] |
YE Xiao-ling, YANG Xing, XIONG Xiong, et al. A quality control method based on an improved random forest algorithm for surface air temperature observations [J]. Adv Meteorol, 2017, 1-15, https://doi.org/10.1155/2017/8601296. https://doi.org/10.1155/2017/8601296.
|
| [23] |
EISCHEID J K, BRUCE B C, KARL T R, et al. The quality control of long-term climatological data using objective data analysis[J]. J Appl Meteorol, 1995, 34(12): 2787-2795, https://doi.org/10.1175/1520-0450(1995)034 < 2787:tqcolt > 2.0.co; 2. DOI: 10.1175/1520-0450(1995)034<2787:tqcolt>2.0.co;2
|
| [24] |
BANNISTER R. A review of operational methods of variational and ensemble-variational data assimilation[J]. Q J R Meteorol Soc, 2017, 143(703): 607-633, https://doi.org/10.1002/qj.2982.
|
| [25] |
YOU Jin-sheng, HUBBARD K G. Quality control of weather data during extreme events [J]. J Atmo Oceanic Technol, 2006, 23(23): 184-197, https://doi.org/10.1175/jtech1851.1.
|
| [26] |
INGLEBY N B, LORENC A C. Bayesian quality control using multivariate normal distributions[J]. Q J R Meteorol Soc, 2010, 119(513): 1195-1225, https://doi.org/10.1002/qj.49711951316.
|
| [27] |
ZHU Fu-xin, CUO Lan, ZHANG Yong-xin, et al. Spatiotemporal variations of annual shallow soil temperature on the Tibetan Plateau during 1983-2013[J]. Clim Dynamics, 2018, 51(5-6): 2209-2227, https://doi.org/10.1007/s00382-017-4008-z.
|
| [28] |
XU Cheng-dong, WANG Jin-feng, HU Mao-gui, et al. Estimation of uncertainty in temperature observations made at meteorological stations using a probabilistic spatiotemporal approach[J]. J Appl Meteorol Clim, 2014, 53(6): 1538-1546, https://doi.org/10.1175/jamc-d-13-0179.1.
|
| [29] |
CERLINI P B, SILVESTRI L, SARACENI M. Quality control and gap-filling methods applied to hourly temperature observations over Central Italy[J]. Meteorol Appl, 2020, 27(3): 1-15, https://doi.org/10.1002/met.1913.
|
| [30] |
CHOI W, HO C H, KIM M K, et al. Season-dependent warming characteristics observed at 12 stations in South Korea over the recent 100 years[J]. Int J Climatol, 2018, 38(11): 4092-4101, https://doi.org/10.1002/joc.5554.
|
| [31] |
LIU Rui-xia, LIU Jie, PATSY A, et al. Preliminary study on the influence of FY-4 lightning data assimilation on precipitation predictions[J]. J Trop Meteor, 2019, 25(4): 110-123, https://doi.org/10.16555/j. 1006-8775.2019.04.009. DOI: 10.16555/j.1006-8775.2019.04.009
|
| [32] |
WHILE J, MARTIN M J. Variational bias correction of satellite sea-surface temperature data incorporating observations of the bias[J]. Q J Roy Meteor Soc, 2019, 145(723): 2733-2754, https://doi.org/10.1002/qj.3590.
|
| [33] |
BORCHMANN D, HANIKA T, OBIEDKOV S. Probably approximately correct learning of Horn envelopes from queries[J]. Discrete Appl Math, 2020, 273(C): 30-42, https://doi.org/10.1016/j.dam.2019.02.036.
|
| [34] |
GOMES H M, BIFET A, READ J, et al. Adaptive random forests for evolving data stream classification[J]. Mach Learn, 2017, 106(9-10): 1469-1495, https://doi.org/10.1007/s10994-017-5642-8.
|
| [35] |
HANKE J R, FISCHER M P, POLLYEA R M. Directional semivariogram analysis to identify and rank controls on the spatial variability of fracture networks[J]. J Structural Geology, 2018, 108: 34-51, https://doi.org/10.1016/j. jsg.2017.11.012. DOI: 10.1016/j.jsg.2017.11.012
|
| [36] |
GUNST R F. Estimating spatial correlations from spatial-temporal meteorological data [J]. J Clim, 1995, 8(10): 2454-2470, https://doi.org/10.1175/1520-0442(1995) 0082.0.co; 2. DOI: 10.1175/1520-0442(1995)0082.0.co;2
|
| [37] |
MADDOX, ROBERT A. An objective technique for separating macroscale and mesoscale features in meteorological data[J]. Mon Wea Rev, 2009, 108(8): 1108-1121, https://doi.org/10.1175/1520-0493(1980) 1082.0.CO; 2. DOI: 10.1175/1520-0493(1980)1082.0.CO;2
|
| [38] |
DENG Shu-lin, CHEN Tan, YANG Ni, et al. Spatial and temporal distribution of rainfall and drought characteristics across the Pearl River basin[J]. Sci Total Environ, 2018, 619-620: 28-41, https://doi.org/10.1016/j. scitotenv.2017.10.339. DOI: 10.1016/j.scitotenv.2017.10.339
|
| [39] |
YUAN Yu-min, CAVE M, ZHANG Chao-sheng. Using local Moran's i to identify contamination hotspots of rare earth elements in urban soils of London[J]. Appl Geochem, 2018, 88: 167-178, https://doi.org/10.1016/j. apgeochem.2017.07.011. DOI: 10.1016/j.apgeochem.2017.07.011
|
| [40] |
CHEN Chen, WEI Zhi-gang, DONG Wen-jie, et al. Quality control and evaluation of flux data of observation platform about land-atmosphere interaction in zhuhai phoenix mountain[J]. J Trop Meteor, 2018, 34(4): 561-569, https://doi.org/10.16032/j. issn. 1004-4965.2018.04.014. DOI: 10.16032/j.issn.1004-4965.2018.04.014
|
| 1. | Liu, P., Xu, Z., Gong, J. et al. A New Progressive EOFs Quality Control Method for Surface Pressure Data Based on the Barometric Height and Biweight Average Correction. Atmosphere, 2023, 14(6): 1032. DOI:10.3390/atmos14061032 |
| Co | Co+C | Ao | R2 | RSS | I | E(I) | mean | sd | z-value | |
| Bh | 0.101 | 0.715 | 1.17 | 0.848 | 0.095 | 0.649 | -0.031 | -0.032 | 0.097 | 7.031 |
| Cd | 0.153 | 2.398 | 1.22 | 0.849 | 1.2 | 0.721 | -0.015 | -0.012 | 0.071 | 10.39 |
| Gz | 0.188 | 1.163 | 2.07 | 0.922 | 0.076 | 0.581 | -0.023 | -0.023 | 0.093 | 6.47 |
| Hk | 0.157 | 0.781 | 1.53 | 0.804 | 0.085 | 0.478 | -0.037 | -0.037 | 0.118 | 4.348 |
| Hh | 0.004 | 2.85 | 0.61 | 0.843 | 2.72 | 0.545 | -0.029 | -0.026 | 0.112 | 5.096 |
| Jh | 0.001 | 2.385 | 0.3 | 0.326 | 13.3 | 0.162 | -0.091 | -0.083 | 0.158 | 1.556 |
| Ls | 0.01 | 6.4 | 0.55 | 0.385 | 79.5 | -0.08 | -0.1 | -0.103 | 0.179 | 0.125 |
| Lz | 0.83 | 4.403 | 0.55 | 0.489 | 4.4 | 0.143 | -0.24 | -0.023 | 0.094 | 1.178 |
| My | 0.51 | 9.029 | 1.48 | 0.876 | 6.55 | 0.729 | -0.013 | -0.013 | 0.065 | 11.43 |
| Mh | / | / | / | / | / | -0.411 | -0.333 | -0.349 | 0.29 | -0.211 |
| Nj | 0.145 | 0.606 | 4.01 | 0.355 | 0.071 | 0.552 | -0.12 | -0.013 | 0.066 | 8.602 |
| Ty | 0.001 | 4.516 | 1.8 | 0.929 | 2.25 | 0.648 | -0.012 | -0.013 | 0.067 | 9.809 |
| Um | 0.01 | 11.58 | 1.54 | 0.371 | 375 | 0.446 | -0.046 | -0.046 | 0.123 | 4.014 |
| Cc | 0.269 | 1.069 | 1.38 | 0.736 | 0.287 | 0.615 | -0.027 | -0.027 | 0.104 | 6.174 |